

Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther and Kritz2000). Reference Hammett, Beer, Dorland, Cowley and Smith1993 Beer & Hammett Reference Beer and Hammett1996 Snyder & Hammett Reference Snyder and Hammett2001) however, these reduced models struggled to accurately predict thermal transport levels, in part due to inaccurate zonal flow dynamics (Rosenbluth & Hinton Reference Rosenbluth and Hinton1998 Dimits et al. These gyrofluid (or Landau fluid) models used sophisticated (but linear) closures to model kinetic effects such as Landau damping and finite Larmor radius (FLR) effects (Hammett & Perkins Reference Hammett and Perkins1990 Hammett, Dorland & Perkins Reference Hammett, Dorland and Perkins1992 Dorland & Hammett Reference Dorland and Hammett1993 Hammett et al. Later, approaches that involved fluid moments of the gyrokinetic equation were developed. Reference Dimits, Williams, Byers and Cohen1996). The first simulation algorithms used for gyrokinetics were particle-in-cell (PIC) algorithms (Lee Reference Lee1983 Kotschenreuther Reference Kotschenreuther1990 Parker & Lee Reference Parker and Lee1992 Dimits & Lee Reference Dimits and Lee1993 Denton & Kotschenreuther Reference Denton and Kotschenreuther1995 Dimits et al. Many gyrokinetic models, algorithms, and codes have been developed and deployed over a period of decades. These micro-instabilities are well described by gyrokinetics (Catto Reference Catto1978 Antonsen & Lane Reference Antonsen and Lane1980 Frieman & Chen Reference Frieman and Chen1982). For the most part, the plasma column itself is macroscopically stable, but these gradients make it prone to microscopic instabilities and non-thermal fluctuations. Steep gradients of density, momentum and temperature are intrinsic to most MCF concepts. Tokamaks and stellarators are magnetic confinement fusion (MCF) concepts which employ toroidal magnetic fields to confine thermonuclear plasmas. Thus the final model is appropriate for the study of instabilities, turbulence and transport in a wide range of geometries, including tokamaks and stellarators. We show that the model is capable of reproducing gyrokinetic results for linear instabilities and zonal flow dynamics.
VELOCITY PHYSICS FREE
Free streaming, magnetic drifts and nonlinear phase mixing each give rise to closure problems, which we discuss in relation to the instabilities of interest and to free energy conservation. While any collision operator can be used in the formulation, we highlight a model operator that has a particularly sparse Laguerre–Hermite representation, while satisfying conservation laws and the H theorem.

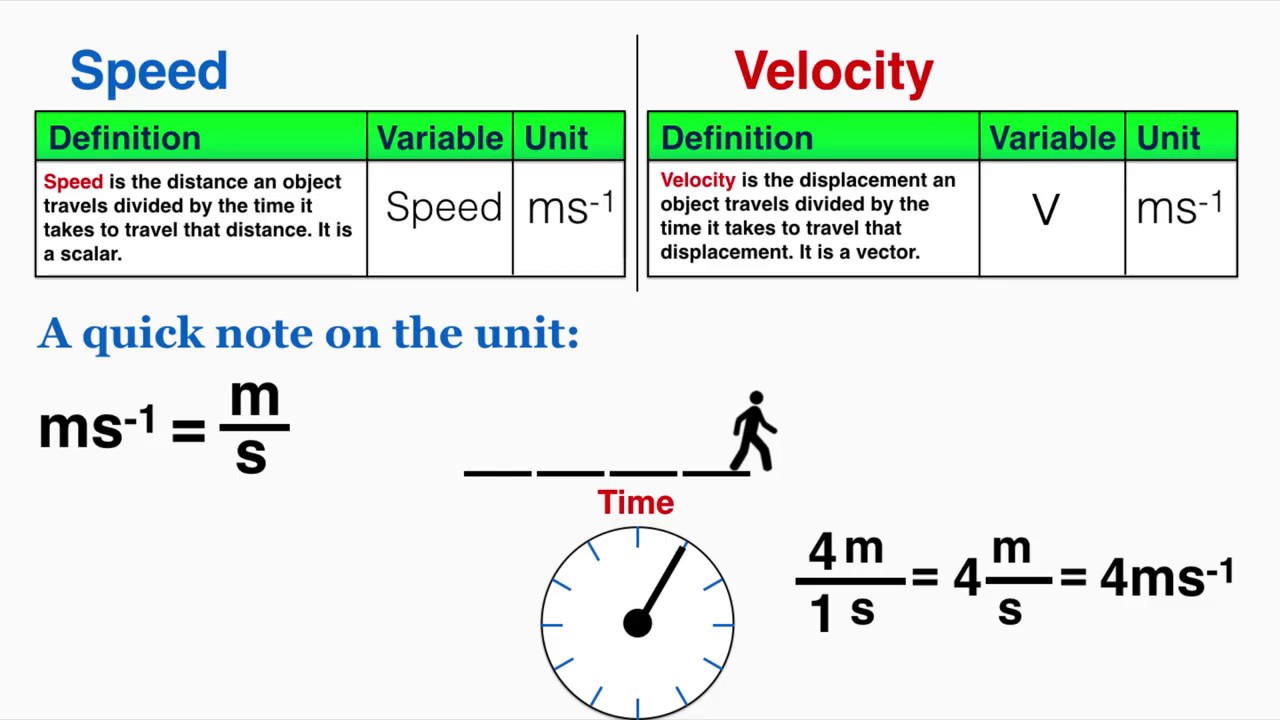
We discuss issues related to collisions, closures and entropy. Our formulation is a projection of the nonlinear gyrokinetic equation onto a Laguerre–Hermite velocity-space basis. We develop a pseudo-spectral velocity formulation of the turbulence equations that smoothly interpolates between the highly efficient but lower resolution three-dimensional (3-D) gyrofluid representation and the conventional but more expensive 5-D gyrokinetic representation. I don't want to have two separate units for that I'm want to simplify that and just let's just keep it hours okay? So instead of saying 60 kilometers in 30 minutes, let's convert 30minutes into hours okay? So I'll say we got 60 kilometers in 0.5 hours that's going to equal 120 kilometers an hour and in this case that's east which is a separate velocity than our initial velocity so answer here we have 100, 75 kilometers an hour north and then 120 kilometers east and that's how we calculate average velocities.First-principles simulations of tokamak turbulence have proven to be of great value in recent decades. Let's say I travel a hundred kilometers north in 2 hours then travel 60 kilometers east in 30 minutes, if this was a speed problem, I could just add those up and divide okay? But this is a velocity problem so I've got to solve that as two separate velocities cause they're not the same okay? So I say 150 kilometers in 2hours that's going to equal 75 kilometers an hour north okay? Then I have 60 kilometers east in 30 minutes, and if you look here I've got hours from my one velocity and minutes from my second. So what's the difference between speed and velocity? Well speed is distance over time 100 kilometers an hour, velocity is very similar 100 kilometers per hour but it's in a specific direction, so 100 kilometers per hour east would be a given velocity okay? Well how do we solve a velocity problem? And how is it different than solving a speed problem?


 0 kommentar(er)
0 kommentar(er)
